“ABC della quarta dimensione” a cura dell’arch. Claude Bragdon

Jorge Luis Borges nel suo articolo “La quarta dimensione” commenta, uno strano libro dell’architetto americano Claude Bragdon. Pubblicato nel 1930 con il titolo “Four Dimensional Vistas” conduce il lettore in un viaggio particolare la cui premessa è affermare che la percezione che abbiamo della realtà è limitata rispetto alla realtà stessa.
Nulla di nuovo insomma. Arriva più di trent’anni dopo il romanzo di fantascienza “La macchina del Tempo” di Wells nel quale si fa largo uso del concetto di quarta dimensione e più di cento anni dopo la scoperta (o l’invenzione se preferite) delle geometrie non euclidee.
Tuttavia, è passato solo un anno dalla pubblicazione delle idee di Einstein che rendono protagonisti gli spazi curvi e multidimensionali nel modello di realtà destinato a sostituire quello newtoniano. Bragdon pensa con ottimismo, l’ottimismo di un Newyorkese degli anni 30, in piena fase mistica, che queste rivoluzioni porteranno a delle modifiche radicali nel modo di pensare dell’uomo; degli scorci di una visione del mondo che renderanno l’uomo meno triste e sofferente. Intravede un futuro in cui non saranno in pochi ad impossessarsi delle idee della scienza e in cui non saranno considerate o come freddi calcoli utili al proprio benessere materiale o come un nuovo sistema di dogmi grazie ai quali pochi accademici potranno nominarsi sacerdoti esoterici di fronte alla massa che ignora.
Ma cosa si intende esattamente quando si parla di quarta dimensione? Come la possiamo vedere?
Un cubo di lato 0 è un cubo che non si vede ma anche un cubo di lato 1 metro che appare per 0 secondi è un cubo che non si vede. Dunque un cubo per poter esistere deve avere 3 dimensioni spaziali e una temporale. Questa la quarta dimensione è il tempo.
Ma possiamo anche valutare una quarta dimensione spaziale: abbiamo a disposizione diversi trucchi: ad esempio come possiamo proiettare un oggetto a 3 dimensioni su una superficie a 2, con una foto, un dipinto, guardandone l’ombra o tagliandone una sezione, possiamo immaginare di mettere in tre dimensioni una figura a 4.
Per cominciare, sfere e cubi vanno bene.
Prendiamo una sfera e intersechiamola con un piano passante per il centro. Il risultato dell’intersezione è un cerchio. Da 3 a 2 dimensioni. Riutilizzando questa proprietà possiamo immaginare come si comporta una sfera a 4 dimensioni: sarà quell’oggetto la cui intersezione con un piano passante per il suo centro è una sfera.

E per il cubo? Il cubo in 4 dimensioni (chiamato anche tesseract da Charles Hinton nel libro “Una nuova era del pensiero” e protagonista di un racconto di David Heinlein e di una storia di Topolino, della quale purtroppo non ricordo il nome, che vedeva Paperino e Archimede alle prese con una casa multidimensionale) possiamo fare qualcosa di analogo. Prima di passare a sezionare il tesseract  possiamo direttamente costruirne uno. Immaginiamo di avere un punto in uno spazio con quattro dimensioni: il punto è sempre uguale a se stesso e non ci crea troppe difficoltà vederlo in 4 o in 100 dimensioni. spostando il punto nello spazio verso una direzione fissata, avanti e indietro possiamo tracciare un segmento. Stiamo usando una delle 4 dimensioni a disposizione, quindi il segmento è ancora lo stesso che possiamo disegnare su un foglio di carta. Ora che abbiamo il segmento lo possiamo spostare in direzione perpendicolare a quella nella quale avevamo mosso il punto. Guadagniamo così una nuova dimensione, la seconda, e otteniamo un quadrato. Ancora pienamente disegnabile su un foglio. Ora muoviamo il nostro quadrato in una dimensione perpendicolare alle prime due usate, e a questo punto avrete già capito dove voglio arrivare.
Usando gli insiemi, e dando delle coordinate ai lati, quello che abbiamo fatto è stato aggiungere un sottoinsieme dei numeri reali ad un prodotto cartesiano:

Segmento:

Quadrato:

Cubo:

Ipercubo:

… e naturalmente Cubo ad n dimensioni:

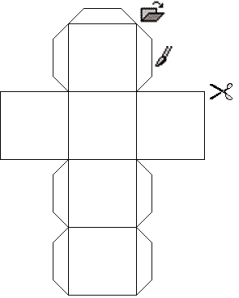
Ma accontentiamoci dell’ipercubo, e prendiamone uno in mano, lo possiamo ricondurre alle tre dimensioni, proiettando le facce. Come è possibile schiacciare le facce di un dado su un piano ottenendo sei quadrati collegati fra loro a formare una croce, è possibile allo stesso modo schiacciare un ipercubo e ottenere 8 cubi collegati fra loro a formare una specie di croce con quattro braccia.
Un altro modo per visualizzare l’ipercubo e proiettare i segmenti che lo definiscono nello spazio. Tenendo in mente che a segmenti paralleli e di uguale lunghezza corrisponderanno nella proiezione segmenti paralleli e di uguale lunghezza, e aiutandoci con zoometool o con dei deciasamente più economici fiammiferi otteniamo qualcosa di simile: